
آزمون بار عرضی (Cross Loading)، یک روش برای محاسبه روایی واگرا در مدل سازی معادلات ساختاری حداقل مربعات جزئی است. چین (۱۹۹۸)، این شاخص را برای محاسبه روایی واگرای هر سازه در مدل حداقل مربعات جزئی پیشنهاد داد. در تحلیل کمترین مربعات جزیی که معمولا با نرم افزار SMARTPLS تحلیل می شود برای روایی واگرا یا تشخیصی که بیانگر وجود همبستگی های جزیی بین شاخص های یک سازه و شاخص های سازه های دیگر است از معیار فورنل و لارکر، آزمون بار عرضی و شاخص HTMT استفاده می شود.
آزمون بار عرضی روایی واگرا را در سطح متغیرهای مشاهده پذیر می سنجد. هنسلر و همکاران (۲۰۱۴)، نشان دادند که در مقالات و تحقیقات انجام شده با نرم افزار SMARTPLS، تنها ۷.۷۹ درصد مقالات تحلیل شده از آزمون بار عرضی برای شناسایی روایی واگرا یا روایی تشخیصی استفاده کردند.
براساس این آزمون، در صورت وجود روایی واگرا، بارهای عاملی هر یک از متغیرهای مشاهده پذیر موردنظر در یک مدل انعکاسی بیشتر از بارهای عاملی متغیرهای مشاهده پذیر دیگر مدل معادلات ساختاری اندازه گیری شده است. بار عاملی هر متغیر مشاهده پذیر (آشکار)، بر روی متغیر پنهان متناظرش، باید حداقل ۰.۱ بیشتر از بارهای عاملی همان متغیر مشاهده پذیر بر متغیرهای پنهان دیگر باشد.
آزمون بار عرضی یکی از خروجی های نرم افزار SMRATPLS 3 است. در نرم افزارهای ورژن پایین تر این شاخص محاسبه می شود. اما در این مقاله به جدیدترین ورژن نرم افزار SMARTPLS توجه شده است. صحت روایی واگرا از طریق این معیار، به این صورت است که مقادیر موجود در روی قطر اصلی ماتریس، باید از کلیه مقادیر موجود در ستون مربوطه بزرگتر باشد.
پس از اجرای مدل، دو صفحه در نرم افزار ظاهر می شود. در صفحه اول، مدل گرافیکی است. در صفحه دوم شاخص های ارزیابی مدل نشان داده شده است. پایین صفحه، ستون Quality Criteria وجود دارد. بر روی گزینه چهارم، Discriminant Validity کلیک کنید. در شکل ۱ این گزینه نشان داده شده است.
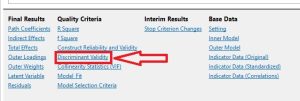
یک پنجره باز می شود که روایی های واگرای بار عرضی و آزمون فورنل و لارکر و شاخص HTMT را نشان داده است. آزمون بار عرضی گزینه دوم در این صفحه است. در شکل ۲ این گزینه نشان داده شده است. همان طور که پیش بینی می شود که بارهای عاملی هرکدام از متغیرهای پژوهش بیشتر از بارهای عاملی مشاهده پذیرهای دیگر مدلهای اندازه گیری موجود در مدل باشد. از طرف دیگر بار عاملی هر متغیر مشاهده پذیر بر روی متغیرپنهان متناظرش حداقل ۱.۰ بیشتر از بارهای عاملی همان متغیر مشاهده پذیر بر متغیرهای پنهان دیگر باشد.
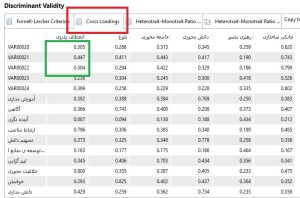
آزمون بار عرضی در عمل برای متغیرهای ناهمگن با اندازه نمونه بالا روایی همگرا را تشخیص می دهد. محققان بیان کردند که آزمون بار عرضی آزادی بیشتری در نشان دادن روایی واگر دارد اما کارایی لازم را در نشان دادن روایی واگرا یا تشخیصی ندارد. این آزمون زمانی که روش فورنل و لارکر نیز توانایی نشان دادن روایی واگرا را ندارد، جوابگو است.
Henseler, J., & Sarstedt, M. (2013). Goodness-of-fit indices for partial least squares path modeling. Computational Statistics, 28(2), 565– ۵۸۰.
برای آموزش آزمون بار عرضی بر روی لینک زیر کلیک کنید.