
روش CRITIC، روش عینی برای تعیین وزن معیارهاست که شامل شدت تضاد و ناسازگاری بین اجزای یک مساله تصمیم گیری است. روش کریتیک توسط دیاکولاکی و همکاران (۱۹۹۵)، ارائه شد. این دو مقوله در آمار به وسیله ضرایب همبستگی و انحراف معیار صورت می گیرد. در واقع انحراف معیار مربوط به مقادیر هر معیار می باشد و ضریب همبستگی مربوط به جفت معیارها می باشد. به عبارت دیگر انحراف معیار در مجموعه صورت می گیرد و همبستگی در خارج از مجموعه.
وزن معیارها از دیدگاه ذهنی خبرگان تاثیر میپذیرد زیرا وزندهی معمولاً توسط تصمیمگیرندگان و براساس تجربه، دانش و درک مساله انجام میشود. با این وجود با بیشتر شدن تعداد معیارها، احتمال خطاهای انسانی و ایجاد شک و تردید در مورد قابلیت اطمینان نتایج نیز افزایش پیدا میکند. در روش کریتیک، برای غلبه بر چنین مشکلاتی از رویکردهای ارزشگذاری عددی استفاده میشود. دو مقوله تضاد و ناسازگاری در آمار بوسیله ضریب همبستگی و انحراف معیار بررسی میشوند. در واقع انحراف معیار مربوط به مقادیر خود معیار بوده و ضریب همبستگی مربوط به زوج معیارها میباشد.
در این روش داده ها براساس میزان تداخل و تضاد موجـود بـین عوامل یـا معیارها مورد تجزیه و تحلیل قرار می گیرند. این شیوه پردازش، باعث می شود که در نتیجه نهایی محاسبات، نقش هر عامل به درستی اعمال گردد. در روش کریتیک برای هـر معیـار ارزیابی دامنه ای از تغییرات مقادیر اندازه گیری شـده در میـان پیکسل ها (گزینه) وجود دارد کـه در قالـب یـک تـابع عضویت بیان می شوند. هر کدام از بـردارهـای تشـکیل شده برای معیارهای مورد استفاده، دارای پـارامترهـای آماری از جمله انحراف معیار هسـتند. ایـن پـارامترهـا نمایــانگــر درجــه تبــاین در مقــادیر معیــار مربوطــه مـی باشـد.
روش CRITIC مخفف Criteria Importance Through Intercriteria Correlation اهمیت معیارها مبتنی بر همبستگی درونی معیارها است. شروط اولیه روش کریتیک عبارتند از:
میزان انحراف معیار در رابطه با هر یک از عاملها نشان از میزان همگنی یا ناهمگنی می باشد. بنابراین انحراف معیار هرچقدر پایینتر باشد می تواند در تنزل وزن، دخیل باشد.
هر اندازه که همبستگی مثبت بین معیارها باهم بیشتر باشد، به همان نسبت تغییرات یک معیار بعنوان معرف، بر تغییرات معیار دیگر توجیه پذیر خواهد بود.
اولین گام در این روش تشکیل ماتریس تصمیم است ماتریس تصمیم این روش همانند ماتریس تصمیم روشهایی چون آنتروپی و دیگر موارد است. در این روش مثبت و منفی بودن معیارها در تعیین وزن دخیل نیست.
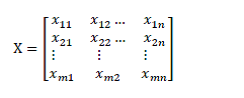
گام دوم در این روش نرمال سازی ماتریس تصمیم است. برای نرمال سازی از رابطه زیر استفاده می شود. با استفاده از این رابطه ماتریس تصمیم نرمال شده و کلیه درایه های آن در بازه صفر تا ۱ قرار می گیرند.
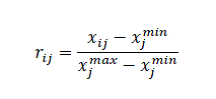
که در آن Wj معرف وزن معیار j و Ci معرف میزان اطلاعات مجموع معیارهای k اسـت کـه از ۱=k شـروع شده وتـا k=m ادامـه دارد. Cj مقدار اطلاعات استخراج شده از معیار j است که از رابطه زیر بدست می آید.
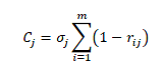
در نهایت وزن نهایی از فرمول زیر به دست می آید:
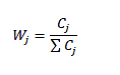
با توجه به روابط فوق، معیـارهـایی کـه دارای Cj بیشـتری باشـند وزن زیــادی بـه خـود اختصــاص خواهند داد. همچنین در رابطه بالا σj انحراف معیار jامین معیار است و rij همبستگی بین دو معیار i و j می باشد.
بر اساس تحلیل فوق، می توان نتیجه گرفت که ارزش بالاتری از Cj مقدار بیشتری از اطلاعات را از معیار داده شده ارائه می دهد بنابراین اهمیت نسبی معیار برای یک مسئله تصمیم گیری مورد توجه بیشتری است.
